Задание 4. Метод Монте-Карло вычисления определённых интегралов.¶

План:

  1. Решим задачу в общем виде и проверим корректность решения на примерах.
  2. Вычислим число $\pi$ с помощью метода Монте-Карло.
  3. Повторим gif-изображение из примера в презентации.

1) Напишем функцию $\texttt{monte\_carlo}$, которая вычисляет определённый интеграл по методу Монте-Карло для некоторой функции $\texttt{f}$:¶

Импортируем необходимые библиотеки:

In [5]:
import random
import math
In [6]:
def monte_carlo(f, a, b, n):
    '''
    f -- функция, определённый интеграл которой требуется вычислить
    a -- начало промежутка интрегрирования [a, b]
    b -- конец промежутка интрегрирования [a, b]
    n -- количество случайных чисел (точность вычисления)
    '''
    random_values = [f(random.uniform(a, b)) for _ in range(n)]  # Случайные значения f(x), равномерно распределенные на отрезке [a, b]
    average = sum(random_values) / n  # Среднее значение функции f(x) для всех n сгенерированных значений x
    return (b - a) * average  # Интеграл f(x) на отрезке [a, b], вычисленный методом Монте-Карло

Проверим работу этой функции на примерах:¶

1. $\int_{0}^{2} x^2 e^x \, dx$¶

Ответ: $2 e^2 - 2 ≈ 12,7781$

2. $\int_{0}^{2\pi} \sin(x) \cos(x) \, dx$¶

Ответ: $0$

In [7]:
def func_1(x):
    return (x ** 2) * math.exp(x)


def func_2(x):
    return math.sin(x) * math.cos(x)


print(f"Первый интеграл: {monte_carlo(func_1, 0, 2, 10000):.4f}")
print(f"Второй интеграл: {monte_carlo(func_2, 0, (2 * math.pi), 10000):.4f}")

Первый интеграл: 12.7169
Второй интеграл: -0.0210

Ответы очень близки, функция $\texttt{monte\_carlo}$ работает корректно! С увеличением $\texttt{n}$ повышается и точность вычисления.

2) Теперь вычислим число $\pi$ с помощью метода Монте-Карло.¶

Методом Монте-Карло можно приближенно вычислить площадь круга. Используя эту площадь, можно приблизительно вычисить число $\pi$:

  1. Сгенерирум случайную выборку точек с координатами $(x,y)$, принадлежащих квадрату со стороной $2$, вписанному в окружность радиуса $1$.
  2. Определим количество точек, попадающих внутрь окружности (расстояние от которых до центра $\leq 1$).
  3. Вычислим отношение количества точек, попавших внутрь окружности, к общему количеству сгенерированных точек.
  4. Приблизительное значение числа $\pi$ равно отношению площади круга $\pi r^2$ к площади квадрата $4r^2$, т.е. $\pi \approx 4 * (\text{кол-во точек внутри}) / (\text{общее кол-во точек})$.
In [8]:
def pi_monte_carlo(n):
    random_x_y = [(random.uniform(-1, 1), random.uniform(-1, 1)) for _ in range(n)]
    inside_circle = 0
    for i in random_x_y:
        if math.sqrt((i[0] ** 2) + (i[1] ** 2)) <= 1:
            inside_circle += 1
    return 4 * inside_circle / n


print(f'{chr(960)} \u2248 {pi_monte_carlo(100000)}')

π ≈ 3.1442

Понятно, что чем больше $\texttt{n}$, тем точнее вычисления и тем ближе ответ к истинному значению числа $\pi$.

3) Напоследок, повторим gif-изображение из примера в презентации:¶

In [ ]:
pip install matplotlib
In [ ]:
pip install IPython
In [6]:
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

Принцип работы этой функции тот же, что и у предыдущей. Основная разница заключается в использовании длины списка со значениями, попадающими внутрь круга, в качестве счётчика, а не простого "$\texttt{inside\_circle += 1}$".

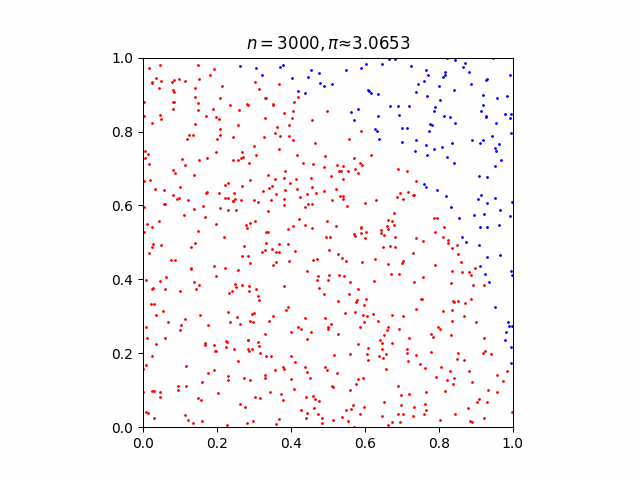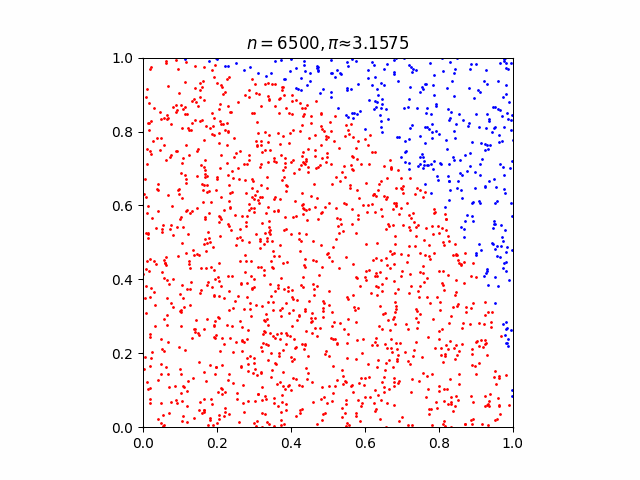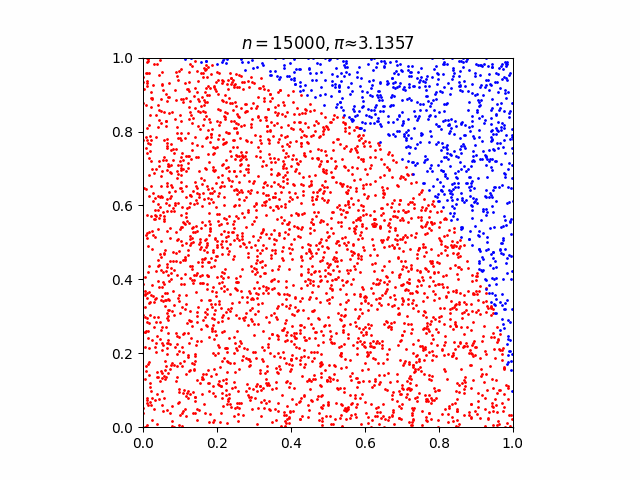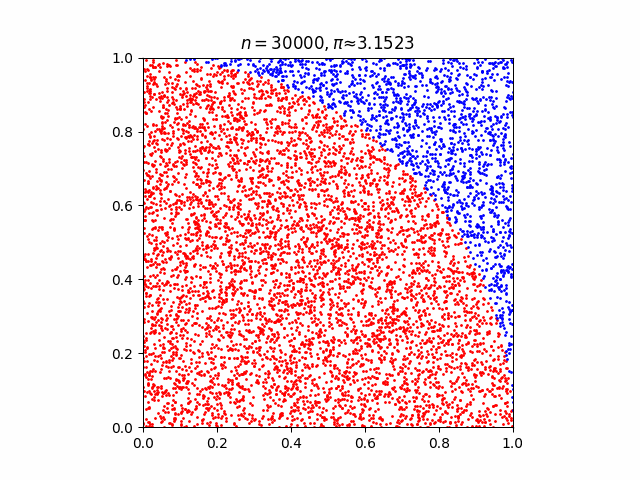
In [10]:
def pi_monte_carlo_plt(n):
    random_x_y = [(random.uniform(-1, 1), random.uniform(-1, 1)) for _ in range(n)]
        
    inside_circle = []
    outside_circle = []
    for i in random_x_y:
        if math.sqrt((i[0] ** 2) + (i[1] ** 2)) <= 1:
            inside_circle.append(i)
        else:
            outside_circle.append(i)

    x_inside = [i[0] for i in inside_circle]
    y_inside = [i[1] for i in inside_circle]
    x_outside = [i[0] for i in outside_circle]
    y_outside = [i[1] for i in outside_circle]

    plt.clf()

    plt.axis('scaled')

    plt.xlim(0, 1)
    plt.ylim(0, 1)
    plt.scatter(x_inside, y_inside, 1, 'red')
    plt.scatter(x_outside, y_outside, 1, 'blue')
    plt.title(f'$n = {n}, \pi \u2248 {(4 * len(inside_circle) / n):.4f}$')


"""Создаём анимацию"""

values = [3000, 4000, 5000, 6500, 8500, 10000, 15000, 18000, 24000, 30000]
anim = FuncAnimation(plt.gcf(), pi_monte_carlo_plt, frames=values, interval=400)
anim.save('pi_monte_carlo.gif', writer='pillow')


"""Заставляем Jupiter Notebook вывести gif-изображение в масштабе 1:1"""

display(HTML('<img src="pi_monte_carlo.gif"  style="image-rendering: pixelated;">'))

plt.close()